- 더 많은 층의 심층 신경망(Deep Neural Network)
- 순방향전파(Forward Propagation)와 역방향전파(Backward Propagation)
- 심층신경망에서의 순방향전파
- 행렬의 차원(크기)을 알맞게 하기
- 심층신경망이 더 많은 특징을 잡아낼 수 있는 이유
- 심층신경망 네트워크 구성하기
- 파라미터 vs 하이퍼파라미터
- 인간의 뇌와의 연관
더 많은 층의 심층 신경망(Deep Neural Network)
심층 신경망은 은닉층이 2개 이상인 신경망이다. 심층신경망의 표기는 다음과 같다.
\[\begin{array}{ll} L & Number\ of\ Layers\\ n^{[l]} & Number\ of\ Units\ in\ Layer\ l\\ a^{[l]} & Activations\ in\ Layer\ l\\ a^{[0]} & Input\ Features\\ a^{[L]} & Predicted\ Output(\ \hat y\ )\\ \end{array}\]순방향전파(Forward Propagation)와 역방향전파(Backward Propagation)
어떤 층 $l$ 에 대한 입력과 출력은 다음과 같다.
\[\begin{array}{ll} Input & a^{[l - 1]}\\ Output & a^{[l]},\ cache(z^{[l]})\\ \end{array}\]그리고 이에 대한 연산은 다음과 같다.
\[\begin{aligned} z^{[l]} &= W^{[l]} \cdot a^{[l-1]} + b^{[l]}\\ a^{[l]} &= g^{[l]}\left(z^{[l]} \right) \end{aligned}\]그리고 이를 벡터화시켜 구현하면 다음과 같다.
\[\begin{aligned} Z^{[l]} &= W^{[l]} \cdot A^{[l-1]} + b^{[l]}\\ A^{[l]} &= g^{[l]}\left(Z^{[l]} \right) \end{aligned}\]순방향전파는 이와 같은 한 층의 연산을 반복하여 여러 층에서의 신경망 연산을 구현한다.
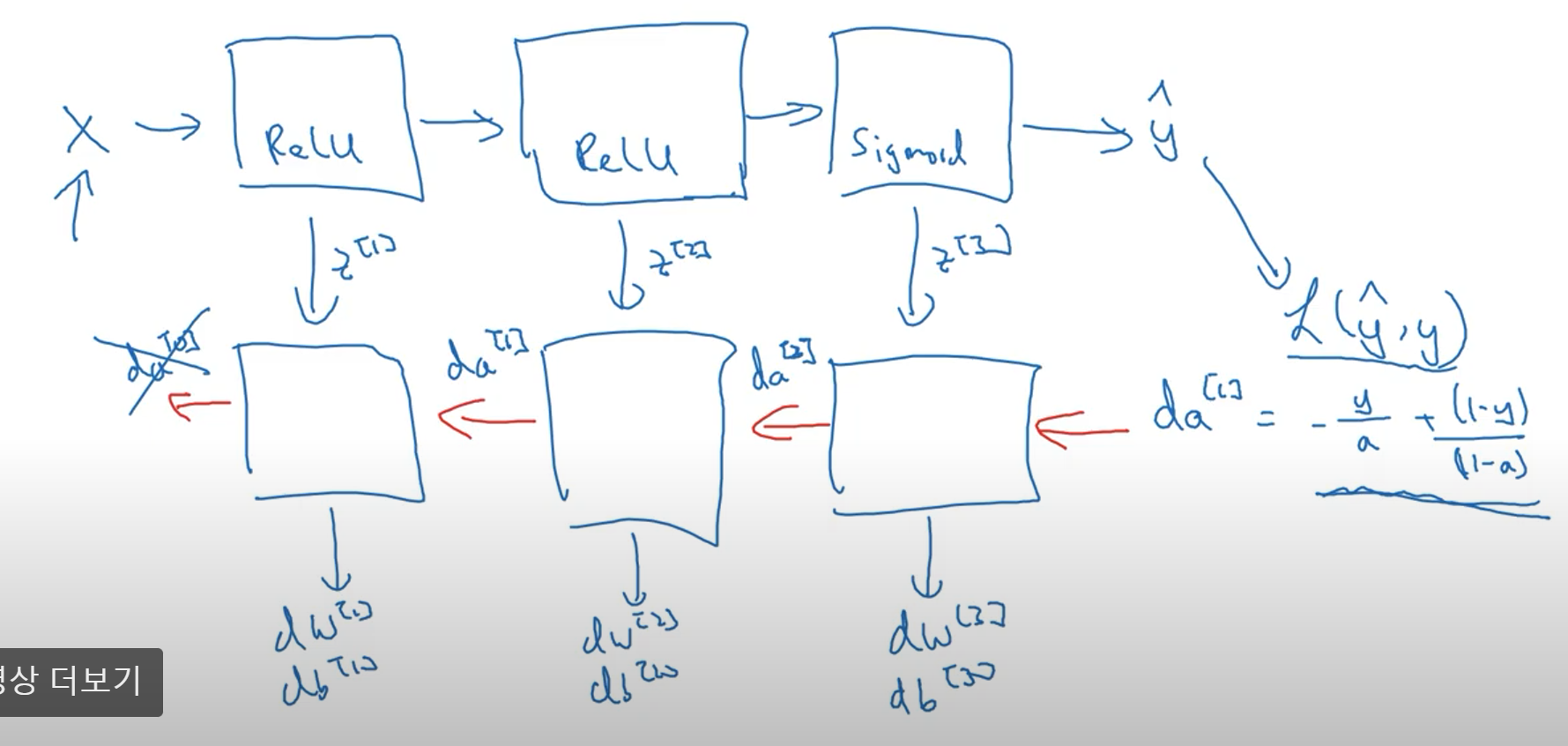
역방향전파는 연쇄법칙(Chain Rule)을 적용하여 파라미터에 대한 미분계수를 구하기 위한 연산이므로, 다음과 같은 입력과 출력을 가진다.
\[\begin{array}{ll} Input & da^{[l]}\\ Output & da^{[l - 1]},\ dW^{[l]},\ db^{[l]},\ cache \left(da^{[l - 1]} \right)\\ \end{array}\]그리고 구현은 다음과 같다.
\[\begin{aligned} dz^{[l]} &= da^{[l]} * g^{[l]} \prime \left(z^{[l]} \right)\\ dW^{[l]} &= dz^{[l]} \cdot a^{[l - 1]}\\ db^{[l]} &= dz^{[l]}\\ da^{[l-1]} &= W^{[l]T} \cdot dz^{[l]}\\ dz^{[l]} &= W^{[l+1]T} \cdot dz^{[l + 1]} * g^{[l]} \prime \left(z^{[l]} \right)\\ \end{aligned}\]이를 벡터화하면 다음과 같다.
\[\begin{aligned} dZ^{[l]} &= dA^{[l]} * g^{[l]} \prime \left(z^{[l]} \right)\\ dW^{[l]} &= \frac{1}{m}\ dZ^{[l]} \cdot A^{[l - 1]T}\\ db^{[l]} &= \frac{1}{m} \sum^{n^{[l]}}_{i = 1} {dZ^{[l]}}_{i}\\ dA^{[l - 1]} &= W^{[l]T} \cdot dZ^{[l]} \end{aligned}\]이는 다음과 같이 시각적으로 표현할 수 있다.
심층신경망에서의 순방향전파
다음과 같은 심층신경망에 대한 순방향전파를 살펴보자.
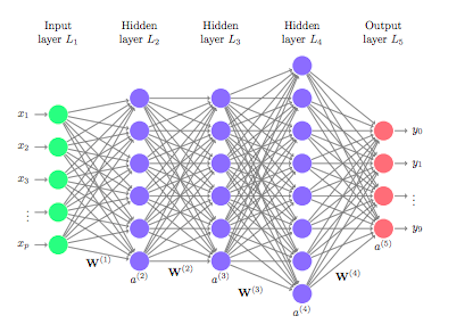
먼저 입력피처 $\mathbb{x}$ 에 대해, 은닉층의 연산은 다음과 같다. (입력층에 대한 인덱스를 제외한 연산이다.)
\[\begin{aligned} x :\ z^{[1]} &= W^{[1]} x + b^{[1]}\\ a^{[1]} &= g^{[1]}\left(z^{[1]} \right)\\ z^{[2]} &= W^{[2]} a^{[1]} + b^{[2]}\\ a^{[2]} &= g^{[2]}\left(z^{[2]} \right)\\ \vdots\\ z^{[4]} &= W^{[4]}a^{[3]} + b^{[4]}\\ \hat y = a^{[4]} &= g^{[4]}\left(z^{[4]} \right) \end{aligned}\]여기서 $x$ 를 $a^{[0]}$ 로 바꾸어도 연산이 잘 정의됨을 확인할 수 있다. 그러므로 신경망의 임의의 층 $l$ 에 대해 일반화된 연산은 다음과 같다.
\[\begin{aligned} z^{[l]} &= W^{[l]}a^{[l - 1]} + b^{[l]}\\ a^{[l]} &= g^{[l]}\left(z^{[l]} \right) \end{aligned}\]입력데이터를 벡터화한 연산도 이 결과를 이용해 쉽게 얻을 수 있다.
\[\begin{aligned} Z^{[1]} &= W^{[1]}X + b^{[1]}\\ A^{[1]} &= g^{[1]}\left(z^{[1]} \right)\\ Z^{[2]} &= W^{[2]}A^{[1]} + b^{[2]}\\ A^{[2]} &= g^{[2]}\left(Z^{[2]} \right)\\ \vdots\\ \hat Y = A^{[4]} &= g^{[4]}\left(Z^{[4]} \right) \end{aligned}\]신경망의 각 층에 대한 반복적인 연산의 경우, 마땅한 벡터화 방법이 존재하지 않는다. 왜냐하면 벡터화는 수학적인 관점에서 선형변환의 일종으로 볼 수 있는데, 신경망의 각 층에서 활성화값을 구할 때 비선형함수에 값을 대입하기 때문에 선형변환으로 표현이 불가하다. 신경망의 한 층에 선형함수를 활성화 함수로 사용하면 그 층은 사라지는 것과 마찬가지임을 지난 수업에서 증명했으므로, 깊은 신경망을 구현하기 위해서는 일반적으로 벡터화가 가능하지 않다. 그러므로 명시적인 반복문으로 구현하는 것도 좋은 방법이다.
행렬의 차원(크기)을 알맞게 하기
심층 신경망 아키텍처를 구현할 때 각 행렬의 차원을 알맞게 하는 것은 중요하다. 그러므로 행렬의 차원을 확인할 필요가 있다. 딥러닝 아키텍처를 다시 살펴보자.

이때 각 층의 $n^{[l]}$ 은 다음과 같다.
\[\begin{aligned} n_x = n^{[0]} &= 5\\ n^{[1]} &= 6\\ n^{[2]} &= 6\\ n^{[3]} &= 8\\ n^{[4]} &= 4\\ \end{aligned}\]그리고 다음의 딥러닝 아키텍처에 대한 순방향전파에 대해,
\[\begin{aligned} z^{[1]} &= W^{[1]}x + b^{[1]}\\ a^{[l]} &= g^{[l]}\left(z^{[l]} \right) \end{aligned}\]각 행렬의 차원은 다음과 같다.
\[\begin{array}{ll} z^{[1]},\ a^{[1]} &: 6 \times 1 = n^{[1]} \times 1\\ x &: 5 \times 1 = n^{[0]} \times 1\\ \end{array}\]그러므로 $W^{[1]}$ 의 크기는 $x$ 와 행렬곱을 했을 때 $n^{[1]} \times 1$ 이 나오도록 하는 크기이어야만 한다. 따라서 파라미터들($W^{[1]},\ b^{[1]}$)의 크기는 다음과 같다. (행렬과 행렬의 합에 대해서는 브로드캐스팅이 적용된다고 가정함.)
\[\begin{array}{ll} W^{[1]} &: 6 \times 5 = n^{[1]} \times n^{[0]}\\ b^{[1]} &: 6 \times 1 = n^{[1]} \times 1\\ \end{array}\]이를 일반화하면 임의의 층 $l$ 의 파라미터들($W^{[l]},\ b^{[l]}$)의 크기는 다음과 같다.
\[\begin{array}{ll} W^{[l]} &: n^{[l]} \times n^{[l - 1]}\\ b^{[l]} &: n^{[l]} \times 1\\ \end{array}\]그리고 역방향전파에서 각 파라미터 행렬의 크기와 이에 대한 미분계수 행렬의 크기는 서로 같으므로, $dW^{[l]},\ db^{[l]}$ 의 크기는 다음과 같다.
\[\begin{array}{ll} dW^{[l]} &: n^{[l]} \times n^{[l - 1]}\\ db^{[l]} &: n^{[l]} \times 1\\ \end{array}\]그리고 $a^{[l]} = g^{[l]}\left(z^{[l]} \right)$ 이므로, $a^{[l]} : n^{[l]} \times 1$ 이다.
데이터셋을 벡터화한 구현에서 파라미터 행렬의 크기는 다르지 않지만 입력피처와 출력의 크기는 달라진다. 데이터셋의 크기 $m$ 에 대해 각 입력과 출력 벡터를 축 1 방향으로 쌓은 것이므로, 각 크기는 다음과 같다.
\[\begin{array}{ll} X &: n^{[0]} \times m\\ Z^{[l]},\ A^{[l]} &: n^{[l]} \times m\\ \end{array}\]역전파에 사용되는 행렬들에 대한 크기도 이와 같다.
\[\begin{array}{ll} {dZ}^{[l]},\ {dA}^{[l]} &: n^{[l]} \times m\\ \end{array}\]심층신경망이 더 많은 특징을 잡아낼 수 있는 이유
여러 층을 가지고 있는 심층신경망은 더 많은 특징들을 인식할 수 있다. 이것이 가능한 이유는 초기층에서는 간단한 특징들을 잡아내고, 이 특징들이 더 깊은 층으로 전달되면서, 층이 더 깊을수록 더 복잡한 특징들을 인식하는 것이 가능해지기 때문이다. 이 덕에 얼굴인식이나 음성인식, 자연어처리 등 다양한 분야에 심층신경망이 큰 힘을 발휘한다. 낮은 층에서는 단순한 특징들을 인식하고, 이를 깊은 층으로 전달하면서, 복잡한 대상들을 인식하고 처리하는 것이 가능해지기 때문이다.
회로 이론을 이용해서도 심층신경망이 왜 잘 작동하는 지에 대한 직관을 얻을 수 있다. 회로 이론이란 어떤 논리 게이트를 이용해서 어떤 종류의 함수를 계산할 수 있을지에 관한 이론이다. 회로 이론에서의 연구에 따르면, 얕은 신경망으로 상대적으로 작은 심층신경망과 같은 성능을 얻기 위해서는 기하급수적으로 많은(지수적 증가를 하는) 은닉층이 필요하다.
심층신경망 네트워크 구성하기
심층신경망의 임의의 층 $l$ 에 대해 파라미터와 순방향, 역방향전파를 다음과 같이 기술할 수 있다.
\[\begin{array}{lll} Parameters\ in\ Layer\ l\ &:\ W^{[l]},\ b^{[l]}\\ \ \\ Forward\ Propagation & Input &:\ a^{[l - 1]}\\ \ & Output &:\ a^{[l]}\\ \ & Cache &:\ z^{[l]}\\ \ \\ Backward\ Propagation & Input &:\ {da}^{[l]}\\ \ & Output &:\ {da}^{[l - 1]}, {dW}^{[l]}, {db}^{[l]}\\ \ & Cache &:\ dz^{[l]} \end{array}\]역방향전파에서는 먼저 순방향전파를 통해 얻은 예측값과 실제 값(Ground Truth)와의 비용함수 값을 역전파하여 파라미터들을 갱신한다. 역전파 과정에서는 먼저 파라미터들에 대한 비용함수의 미분계수 행렬을 구하고, 미분계수 행렬과 다음의 식을 이용해 파라미터를 갱신한다.
\[\begin{aligned} W^{[l]} &:= W^{[l]} - \alpha\ {dW}^{[l]}\\ b^{[l]} &:= b^{[l]} - \alpha\ {db}^{[l]}\\ \end{aligned}\]이 과정을 반복하면서 비용함수값을 최소화하면 학습이 진행된다.
파라미터 vs 하이퍼파라미터
머신러닝에서 파라미터의 예로는 가중치($W^{[l]}$)와 편향($b^{[l]}$)이 있다. 하이퍼파라미터로는 학습률($\alpha$), 경사하강법의 반복 횟수, 은닉층의 갯수 등이 있다. 하이퍼파라미터와 파라미터의 종류를 다음과 같이 나열해보자.
\[\begin{array}{lll} Parameters & W^{[1]},\ b^{[1]},\ W^{[2]}, b^{[2]},\ \cdots\\ Hyperparameters & \alpha &: Learning\ Rate \\ \ & L &: Number\ of\ Hidden\ Layers\\ \ & n^{[1]},\ n^{[2]},\ \cdots &: Number\ of\ Hidden\ Units\\ \ & ReLU,\ tanh,\ Sigmoid,\ \cdots &: Choice\ of\ Activation\ Function\\ \ &\ &: Number\ of\ Iterations\\ \ & \ \vdots \\ \end{array}\]이 특별한 파라미터들은 파라미터들을 결정한다. 그래서 하이퍼파라미터라고 부른다. 우리가 지금까지 살펴본 파라미터들 외에도 다른 하이퍼파라미터들이 존재한다. 하이퍼파라미터를 결정하는 일반적이고 명확한 방법론은 지금까지 존재하지 않는다. 그래서 다양한 하이퍼파라미터들을 조합하고 적용하면서 경험적으로 결과를 얻는다. 이는 딥러닝에서 매우 아쉬운 점이지만, 딥러닝 분야가 발전함에 따라 더 좋은 방법들이 나타날 것이다.
인간의 뇌와의 연관
딥러닝과 인간의 뇌는 어느정도 연관이 있다. 딥러닝 아키텍처의 하나의 유닛은 생명체의 신경망의 뉴런과 기능이 거의 유사하다. 하나의 뉴런의 기능은 복잡하기 때문에 오늘날에도 거의 밝혀내지 못하고, 인간의 뇌가 학습할 때 역전파를 사용하는 지도 불분명하다. 따라서 뇌에 대한 비유는 적절하지 않은 경우가 많다. 하지만 딥러닝의 초기에는 인간의 뇌에서 많은 영감을 받았다.
본 노트는 Andrew Ng의 머신러닝 수업을 정리한 것임. Andrew Ng, Machine learning lecture, Youtube Link
이전 포스트